Previously, we talked about [Pinhole Obsession](https://www.tangramvision.com/blog/camera-modeling-pinhole-obsession) and the downsides of assuming a default pinhole model. We presented an alternative formulation where rays are modeled on the unit sphere \\(\mathcal{S}^2\\) instead of the normalized image plane \\(\mathbb{T}^2\\).
We’ve also previously written posts about how many problems in robotics can be formulated as [an optimization](https://www.tangramvision.com/blog/introduction-to-optimization-theory). At a high level, many continuous optimization algorithms perform the following steps
– Compute a quantity to minimize — error, misalignment, risk, loss, etc.
– Compute a direction along which the quantity is locally reduced
– Move the parameters in the quantity-reducing direction
– Repeat until the problem converges
Many continuous optimization problems are modeled on [vector spaces](https://en.wikipedia.org/wiki/Vector_space) and “moving” the parameters is simply vector addition. However, our prescription of using the unit sphere to model rays is obviously **not** a linear space! Therefore, we must start our discussion by describing how to travel on the sphere.
## Traveling on the Sphere
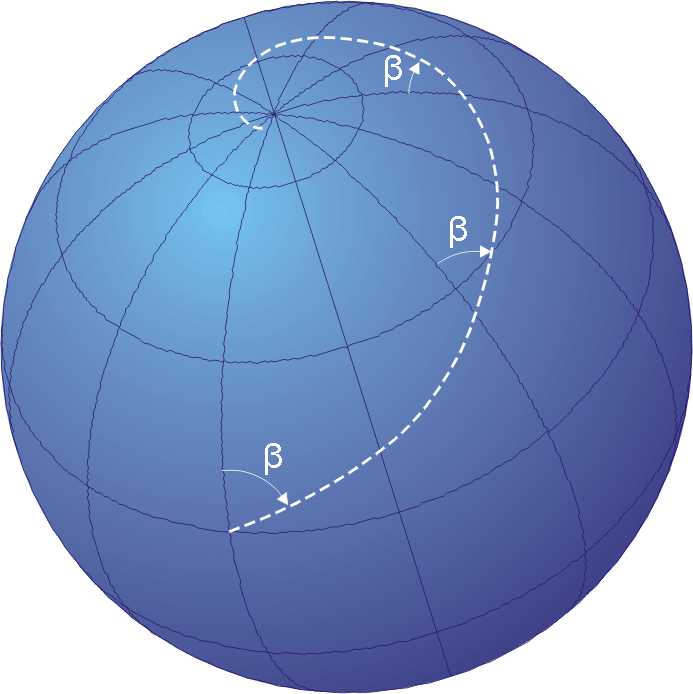
Generally, when we *travel* we want to do so in the most efficient manner. Undoubtedly, you’ve heard the expression “get from point a to b,” perhaps also with the implication “as fast as possible.” Therefore, we’ll want to minimize the distance that we travel or equivalently travel along the shortest path. In Differential Geometry, we call these “shortest paths” *geodesics.*
An alternate way to view a *geodesic* is by starting at a point \\(p\\) on the manifold and traveling in the direction of some vector \\(v\\), carefully minimizing the distance at each increment. However, minimizing the distance at each step may mean we have to *change direction* along our shortest path.
“Changing direction” and “traveling in the shortest path” may seem to counter one another. After all, we all know that the shortest path between two points is a line. However, imagine we are flying in a plane starting at the equator and a heading of 45°. If our goal is to travel *as far as possible* from our starting point, how should we chart our course?
> As usual, ignore air resistance, the jet stream and assume a spherical earth. This is a thought exercise, not pilot’s school.
A simple suggestion would be to maintain a heading of 45° during our travel, like we would locally: travel in a constant direction. However, if we maintain a fixed heading indefinitely, we will end up close to the north pole! The line traced by a path of constant heading is known as a [Rhumb Line](https://en.wikipedia.org/wiki/Rhumb_line) and, as pictured, is certainly not the shortest distance between two points on a sphere.
*PC: [https://en.wikipedia.org/wiki/Rhumb_line#/media/File:Loxodrome.png](https://en.wikipedia.org/wiki/Rhumb_line#/media/File:Loxodrome.png)*
Alternatively, to truly travel the *farthest distance,* we travel along the [great circle](https://en.wikipedia.org/wiki/Great-circle_distance) until the aircraft runs out of fuel. Here it’s more obvious that the geodesic’s heading is continuously changing. One implication of this is that if we start at one point along the geodesic with a vector \\(v\\), we may not end up in the same location as if we start at a different point along the geodesic with the same vector \\(v\\).

*PC: [https://en.wikipedia.org/wiki/Great-circle_distance#/media/File:Illustration_of_great-circle_distance.svg](https://en.wikipedia.org/wiki/Great-circle_distance#/media/File:Illustration_of_great-circle_distance.svg)*
In Differential Geometry, the operator that traces the geodesic is known as “the exponential map.” For the reasons listed above, it’s defined as a local operator originating at a point \\(p\\) and traveling in a direction \\(v\\) i.e.
$$
\text{Exp}_p(v)
$$
Similarly, the operator that computes the direction and distance between two points on the manifold (the manifold’s logarithm) is defined as a local operator \\(\text{Log}_p(q)\\).
So to perform optimization on the unit sphere, we
– Compute the quantity to minimize — error, misalignment, risk, loss, etc.
– Compute a direction \\(v\\) along which the quantity can be locally reduced
– Move the parameters along the great circle using the exponential map \\(\text{Exp}_p(v)\\)
– Repeat until the problem converges
This begs the question: how do we compute this direction \\(v\\)? What does it really mean?
—
## The Briefest Introduction to Differential Geometry
> ⚠️ Many maths below! But they’re cool maths, we promise.
To explain what a direction \\(v\\) means on the sphere and to explain why working with \\(\mathcal{S}^2\\) is difficult, we have to briefly touch on one of my favorite subjects: [Differential Geometry](https://en.wikipedia.org/wiki/Differential_geometry). This post will dive deep into the motivations behind why we use differential geometry in computer vision, and what advantages it brings. Much of this may seem like a tangent (no pun intended), but don’t worry: we’ll bring it all back to our Pinhole Obsession and optimization at the end!
> 💡 Obviously, we cannot cover the entirety of Differential Geometry in one blog post. There are many great resources to learn Differential Geometry. Some of our favorites are:
> – [Introduction to Smooth Manifolds](https://link.springer.com/book/10.1007/978-1-4419-9982-5)
> – [A Micro Lie Theory for State Estimation in Robotics](https://arxiv.org/pdf/1812.01537)
> – [Differential Geometry and Lie Groups](https://link.springer.com/book/10.1007/978-3-030-46040-2)
Historically, differential geometry arose from the study of “curves and surfaces.” As traditionally taught in multi-variable calculus, a curve is a mapping \\(\gamma: \mathbb{R} \to \mathbb{R}^3\\) and likewise, a surface is a mapping \\(\sigma: \mathbb{R}^2 \to \mathbb{R}^3\\).
Differential geometry generalizes these “curves and surfaces” to arbitrary dimensions. These generalized “curves and surfaces” are known as *smooth manifolds*. In this post, we’ll skip the rigorous definition of a smooth manifold and simply define it as
> *Smooth Manifold:* An N-dimensional space without corners, edges or self-intersections.
This smoothness (called continuity) allows us to perform optimization “on the manifold” using our standard calculus techniques. We can compute errors and also compute the directions along which we can reduce those errors.
## Intrinsic vs Extrinsic Manifolds
To assist intuition, we’ve leaned on prior knowledge of multi-variable calculus of curves and surfaces. At the undergraduate level, curves and surfaces are presented as [embedded entities](https://en.wikipedia.org/wiki/Nash_embedding_theorems) living in a higher-dimensional ambient space e.g. 3D Euclidean Space. However, this ambient space isn’t *strictly* needed for the development of differential geometry. In their search for a minimal set of axioms, differential geometers have taken great care to remove this dependence on an ambient space; they describe *smooth manifolds* as objects existing in their own right. Thus, there are two ways of thinking about differential geometry:
– *Extrinsic*: manifolds as embedded objects in space
– *Intrinsic*: manifolds are entities in their own right
In this manner, the error-minimizing direction we are searching for can either be viewed as *extrinsic* (embedded in ambient space) or it can be viewed as *intrinsic* (living alongside the manifold).
As engineers, the decision to use the intrinsic view of a manifold vs. the extrinsic view mostly impacts representation and computation. Thus, for a specific manifold, we choose the representation that’s computationally easiest to work with. Although the remainder of this post only briefly touches on the representation of manifolds, it’s **always** necessary to determine what representation is being used. The decision of an intrinsic or extrinsic representation will change how computation is performed on the manifold. Regardless of the choice of *intrinsic* or *extrinsic* representation, we often “bundle” the representation of the manifold with the representation directions on that manifold.
> ⚠️ The concepts of *intrinsic* and *extrinsic* used in differential geometry are unrelated to intrinsics (interior orientation) and extrinsics (exterior orientation) of cameras. This is simply an unfortunate naming collision at the intersection of two fields.
## A Brief Tangent for Tangents
…which brings us to **the** key concept in differential geometry: the [Tangent Bundle](https://en.wikipedia.org/wiki/Tangent_bundle). The Tangent Bundle is the underlying manifold stitched together with the vector spaces that are tangent to the manifold at each point.
To illustrate this, consider the unit circle \\(\mathcal{S}^1\\) below. The blue circle represents the underlying manifold and the red lines represent the one dimensional tangent space at each point on the circle. Together, the points and tangent spaces form the tangent bundle. It is important to note that that vectors in one tangent space should be regarded as distinct and separate from vectors in another tangent space.

*PC: [https://commons.wikimedia.org/wiki/File:Tangent_bundle.svg](https://commons.wikimedia.org/wiki/File:Tangent_bundle.svg)*
Now that we have the correct picture in our heads, let’s visualize tangent vectors and the tangent bundle in more detail.
Consider an arbitrary manifold \\(M\\), and furthermore consider a curve on that manifold \\(\gamma: \mathbb{R} \to M\\). This curve \\(\gamma(t)\\) can be thought of “the location on the manifold at time \\(t\\).” Furthermore, let \\(\gamma(0)\\) be some point of interest \\(p \in M\\) on the manifold.
For visualization, consider this wavy circle manifold:

Now, consider the curve \\(\gamma(t)\\) living on this manifold.
If we take the derivative of this curve, we obtain a pair \\((\gamma(t), \gamma'(t))\\), where the first entry describes the point along the curve and the second entry describes how the curve is changing in time. This can be visualized as a vector “riding along” the curve.
The magnitude and sign of this vector can be changed by re-parametrizing the curve as
$$\gamma_{\alpha}(t) = \gamma(\alpha t)$$
Specifically, note that
$$\gamma’_\alpha(0) = \alpha \gamma'(0)$$
In this manner, we can “scale” curves in the same way that we would scale vectors. Similarly, we can derive addition, inverse and zero curves and form a “vector space of curves.”
Thus, we define the tangent space \\(T_pM\\) as the set of all curves that pass through a point of interest \\(p \in M\\). The tangent bundle of a manifold \\(TM\\) is the set of all tangent spaces combined under a *disjoint* union. In this context, a disjoint union simply means we cannot combine vectors in distinct tangent spaces. This is perhaps the most important takeaway: tangent vectors living in distinct tangent spaces cannot be added, combined or related without using some additional manifold structure.
> ⚠️ Here, we have *de facto* assumed that we can take the derivative of a curve on the manifold. This is made more rigorous in most differential geometry books by either using charts on the manifold or an extrinsic view of a manifold facilitated by an embedding. Furthermore, we didn’t really show how to “add curves.” We haven’t done anything *improper* with this explanation, but it certainly is lacking detail! You can refer to the previously mentioned resources to learn more about the mathematically precise definitions of the Tangent Bundle.
If this is your first time studying Differential Geometry, you may be very uncomfortable with the notion of a vector being *attached* in any way to a specific point. After all, vectors are commonly taught as being geometric entities that can be moved anywhere in space, e.g. vector addition is taught using the “head to tail” method. It’s unclear when presenting these geometric explanations if the vectors are “sitting on top of” the underlying manifold or if they are in their own “vector space.”
To see why this “head to tail” method breaks down on manifolds, imagine traveling 1000 miles north and then 1000 miles west. This will take you to a very different location than if you had traveled 1000 miles west and then 1000 miles north. In other words, vectors may point in different directions at different points on the manifold, so we can only really discuss what a vector means *locally*.
The representation we have presented here of \\((\gamma(0), \gamma'(0))\\) , is useful in describing the construction tangent vectors on a manifold and also useful in derivations of certain operators, but it is typically not used in computation. In “the real world,” we typically choose some canonical coordinates for the manifold and a basis for the associated tangent space and think of tangent vectors as \\((p, v) \in M \times \mathbb{R}^n\\).
With this understanding of tangent spaces, the exponential map can be understood more formally as an operator mapping vectors in a tangent space onto manifold.
$$
\text{Exp}_p(v): T_pM \to M
$$
Likewise, the logarithmic map can be understood as an operator mapping points on the manifold back into a tangent space
$$
\text{Log}_p(q): M \times M \to T_pM
$$
> 🚧 Ok, *technically*, more structure is needed for the existence of an exponential map. Since the exponential map minimizes distance along a path, we must have some notion of *length.* The subfield of Differential Geometry with *lengths* and *angles* is called [Riemannian Geometry](https://en.wikipedia.org/wiki/Riemannian_geometry) and is a fascinating subject in its own right. The definition of *lengths* and *angles* for a specific manifold is called the Riemannian Metric. We don’t have the space in this post to develop these ideas fully but we encourage the motivated reader to learn more!
With this understanding, we have the following prescription for optimization on a generic manifold \\(M\\)
– Compute the quantity to minimize — perhaps using our logarithmic map \\(\text{Log}_p(q)\\)
– Compute a direction \\(v\\) in \\(T_pM\\) along which the quantity is locally reduced
– Move the parameters using the exponential map \\(\text{Exp}_p(v)\\)
– Repeat until the problem converges
At this point, you are probably saying
> “Why isn’t multi-variable optimization taught like this?”
> “I haven’t had to worry about *tangent spaces* and *exponential maps* before.”
> “Adding vectors has always *just worked* for me in the past.”
Yes, BUT. The secret here is that you’ve been exploiting a very special property of euclidean space: *continuous symmetry* of its tangent bundle.
## Continuous Symmetry
Some smooth manifolds exhibit a natural symmetry. By symmetry, we mean a concept that implies more than reflections or rotations of polygons taught in grade school. For instance, reflections and rotations of polygons are examples of *discrete symmetry.* However, in the study of smooth manifolds, we are interested in *continuous* *symmetry* of the Tangent Bundle. This is what makes optimization so simple in euclidean space.
To illustrate, consider the smooth manifold of real numbers of dimension \\(n\\): \\(\mathbb{R}^n\\) or Euclidean Space. We will visualize the plane \\(\mathbb{R}^2\\), but realize that these properties apply in higher dimensions, too.
Let’s place a uniform vector field on \\(\mathbb{R}^n\\), where “the same” vector \\(v\\) is attached to each point in the space \\(p\\). Imagine those points *flowing* along the vectors, as if the vectors describe the current of a river and the points are rafts in that river.
You’ll notice that the points before and after the flow are effectively the same! Since this flow doesn’t *fundamentally* change the total set of points, it’s called an *invariant flow.*
Now let’s flip it: instead of moving each point along the flow of individual vectors, let’s recenter the points on a new origin.
Notice that this recentering effectively produces the same transformation as the vector field above. This is one important property of continuous symmetry of the manifold: the equivalence of local transformations under *constant* vector fields and global transformations of the entire space.
We can also recenter both the vector field and its associated points. Doing so, we find that the points and vector field are fundamentally *unchanged.*
Furthermore, the points and vector field don’t have to be recentered in the same direction as the vector field. Under any arbitrary translation, the points and the *constant* vector field remain unchanged*.* In this way, both the manifold and the Tangent Bundle exhibit continuous symmetry.
So to recap, when we say *continuous symmetry* of the tangent bundle of \\(\mathbb{R}^n\\) we mean three things:
– Local flows along an invariant vector field are the same as a global translation of all points
– Arbitrary translations of points yields the same set of points
– Arbitrary translations of *constant* vector fields yields the same *constant* vector field
One consequence of this continuous symmetry is that we can effectively treat *any* point in \\(\mathbb{R}^n\\) as the origin. To illustrate this, we will “subtract” two points \\(p\\) and \\(q\\) and get a vector pointing from \\(p\\) to \\(q\\), and then flow \\(p\\) along the vector to recover \\(q\\).
If we follow this animation *carefully,* we have to remember that this red vector lives in \\(T_p\mathbb{R}^n\\) and then *flow* the point starting at \\(p\\) until it reaches \\(q\\). Now, let’s first recenter the origin at \\(p\\) and then perform the subtraction.
We see that this produces the *same* result, and this time the vector was “attached to the origin.” In effect, we can do the subtraction *as if* the space was centered at \\(p\\) and then only worry about vectors living in \\(T_0 \mathbb{R}^n\\).
You probably didn’t realize it, but we’ve set ourselves up for easy computation! If we use the standard basis of \\(\mathbb{R}^n\\), we simply subtract the coordinates of each point element-wise to get the vector. If we want to translate a point by a vector, we again can simply perform element-wise addition of the coordinates. The annoying book-keeping that comes with this vector distribution is effectively non-existent, because we just treat all vectors *as if* they lived in the tangent space at the origin.
In fact, since \\(T_0\mathbb{R}^n\\) is essentially just a copy of \\(\mathbb{R}^n\\), we can confuse points and vectors and likely *get away with it*. The distinction between a point and the vector that points from the origin to a point is so subtle that in practice it’s often not worth mentioning.
Using the continuous symmetry of \\(\mathbb{R}^n\\) we formulate our optimization steps as
– Compute the quantity to minimize *as if* our parameters represent the origin
– Compute a direction along which the quantity is locally reduced
– Add the minimizing direction to our parameters *as if* our parameters represent the origin
– Repeat until the problem converges
With continuous symmetry in euclidean space on our side, we can use the \\(\mathbb{R}^n\\) hammer on *everything*. Recalling our [previous post](https://www.tangramvision.com/blog/camera-modeling-pinhole-obsession): consider \\(\mathbb{T}^2\\). You’ll notice now that it is essentially \\(\mathbb{R}^2\\) with a couple of “extra points at infinity.” This makes computer vision with camera rays and the pinhole camera model feel easy! We just treat \\(\mathbb{T}^2\\) as \\(\mathbb{R}^2\\) and compute reprojection error by subtracting points and minimizing that error.
## Lie Groups: *Continuing* the Symmetry Party
But, I hear you mutter to yourself,
> “Are there manifolds that have continuous symmetry of their Tangent Bundle, but are not flat like \\(\mathbb{R}^n\\)?”
Great question! The answer is yes! An example of manifolds that fit these criteria are [Lie Groups](https://en.wikipedia.org/wiki/Lie_group). A Lie Group (we’ll call it \\(\mathcal{G})\\) is a [mathematical group](https://en.wikipedia.org/wiki/Group_(mathematics)) that is also a smooth manifold.
Many commonly-used manifolds in robotics are Lie Groups:
– Special Orthogonal Group \\(SO(3)\\) – used for describing rigid-body rotations
– Special Euclidean Group \\(SE(3)\\) – used for describing rigid-body motion
– Special Linear Group \\(SL(3)\\) – used for describing continuous-time homographies
– Similarity Group \\(Sim(3)\\) – used for describing similarity transforms (rigid-body + scale)
Given their wide usage, it’s worthwhile to explore what makes them so useful.
A Lie Group is a mathematical group; it’s in the name. This means it has a way to compose elements, typically denoted as \\(g \circ h\\) for group elements \\(g,h \in \mathcal{G}\\). Additionally, the group has an identity element (typically called \\(e\\)). In some fashion, this identity can be considered the “origin”. Since a Lie group is *also* a smooth manifold, it has a tangent space at this “origin.” The tangent space at the identity element is called the [Lie Algebra](https://en.wikipedia.org/wiki/Lie_algebra) and is denoted by \\(T_e \mathcal{G} = \mathfrak{g}.\\)
To help us develop some intuition of Lie Groups, we will consider the simplest non-euclidean Lie Group, the unit circle \\(\mathcal{S}^1\\) and its associated Lie Algebra. Note that unlike our visualization of \\(\mathbb{R}^n,\\) we have chosen to explicitly display a tangent space of unit circle, since it takes a different shape than the underlying manifold.

Now, we proceed to choose some vector in this tangent space at the identity.
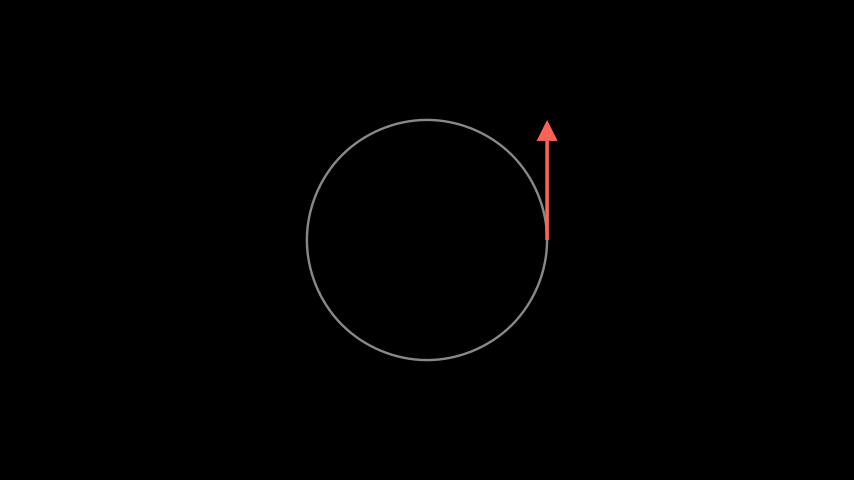
Now, let’s try to move a point along our chosen vector.
If we simply move the point along the vector, the point leaves the manifold! This is not a valid flow, because the points must *by definition* live on the underlying manifold. To fix this, we will define the *flow* as the curve \\(\varphi(t)\\) such that \\(\varphi'(t)\\) matches the tangent vector. For a vector field \\(X\\) defined on the entire manifold, we denote this flow as \\(\varphi_X(t)\\).
However, this definition makes solving for \\(\varphi_X(t)\\) a bit tough since we have to solve an ordinary differential equation on a manifold. If we instead think of Euler integration, we can *approximate* a solution by “moving along” the manifold in the direction of the vector field.
In \\(\mathbb{R}^n\\), for a given vector field \\(X: \mathbb{R}^n \to T\mathbb{R}^n\\) euler integration gives us the recurrence of
$$
p_k = p_{k-1} + X(p_{k-1}) \Delta t
$$
On the manifold we can use the exponential map to similar effect. For a given vector field \\(X: M \to TM\\) “euler integration” takes the form of
$$p_k = \text{Exp}_{p_{k-1}}(X(p_{k-1})\Delta t)$$
We can imagine this exponential map as a “pushed down” vector on the manifold.
> ⚠️ In actuality, there is no such thing as a “pushed down vector,” however it’s a useful concept for visualization. If we use the definition of the exponential map, we can imagine this “pushed down vector” as the line drawn by the equation \\(\text{Exp}(\alpha v)\\) for a fixed vector \\(v\\) and a scalar \\(\alpha \in [0,1]\\).
Now following our example with \\(\mathbb{R}^2\\), let’s try to create a *constant* vector field by copying a vector into all points on the manifold. If we naively copy this vector in the same way that we did in the euclidean case (remember that big grid of arrows?), we get the following:

This cannot be correct; our vectors wouldn’t live in their own respective tangent spaces. These “tangent vectors” have some component pointing normal to the manifold, which implies they are not tangent vectors at all! How do we address this mathematically?
> ⚠️ Here we are claiming that this visualization is incorrect because we are considering the unit circle and its tangent bundle as entities *embedded* in ambient euclidean space \\(\mathbb{R}^2\\). In reality, we only care about the geometric and algebraic structure of the unit circle and our visualization is *somewhat independent* of that structure. It it not uncommon to visualize a manifold and an associated fibre bundle (e.g. the tangent bundle) as living in orthogonal spaces but connected at a single point. This explains why you sometimes may see the tangent bundle visualized as a manifold with non-overlapping tangent spaces.
> 
*PC: [https://commons.wikimedia.org/wiki/File:Tangent_bundle.svg](https://commons.wikimedia.org/wiki/File:Tangent_bundle.svg)*
> In this post, we’ll continue with the embedded and overlapping view to aid intuition, but don’t be surprised if you see the tangent bundle drawn differently in other resources.
Instead of naively copying the vector at identity to every point on the lie group, let’s consider an arbitrary point \\(g \in \mathcal{G}\\). We can consider this point on the manifold as simply a point or, using the group structure, we can consider it as an operator since \\(g \circ e = g\\). In other words, \\(g\\) can be regarded as an operator that takes the identity into \\(g\\). This “operatorness” of \\(g\\) is typically denoted as the map
$$
\begin{aligned}
L_g: \mathcal{G} &\to \mathcal{G} \\\\
h &\mapsto g \circ h
\end{aligned}
$$
where the \\(L\\) denotes that we are composing with \\(g\\) on the left. You can form a similar map by composing on the right; we’ll call it \\(R_g\\).
We can use this operator concept to “push” vectors around on the manifold. Instead of \\(L_g\\) operating on a fixed value \\(h\\), we can imagine it operating on a curve \\(\gamma(t)\\) with \\(\gamma(0) = h\\).
Now we have a new *shifted* curve
$$
L_g(\gamma(t)) = g \circ \gamma(t)
$$
We can now consider the derivative of this new *shifted vector* as a vector living in the tangent space \\(T_{g \circ h} \mathcal{G}\\):
$$
\frac{d}{dt}L_g(\gamma(t))\vert_{t=0}
$$
…just like we did in our original vector field in \\(\mathbb{R}^n\\). For convenience of notation, we’ll drop the explicit parametrization of the curves and denote this vector shift as \\(dL_g(h,v)\\) for some \\(v \in T_h \mathcal{G}.\\)
💡
The argument made here to derive this vector shift function actually extends to arbitrary manifolds. If we have an map between manifolds
$$
\begin{aligned}
f: M \to N
\end{aligned}
$$that obeys the continuity properties of the manifold, we can create an induced map on the tangent bundle
$$
df: TM \to TN
$$This induced map is often referred to as the differential or “push forward” map because it “pushes” vectors in tangent spaces of one manifold onto tangent spaces of another manifold.
Now, we will state a few facts without proof about \\(dL_g(h,v)\\)
1. \\(dL_g(h,v)\\) is linear in \\(v\\)
2. \\(dL_g(h, v)\\) actually does not depend on \\(h\\), so we can write it as \\(dL_g(v)\\)
3. \\(dL_g(dL_h(v)) = dL_{g \circ h}(v)\\) or in other words group composition is compatible with vector shifting.
Got all that? Good! Now that we have this structure in place, let’s return to our tangent vector at the origin.

This time we will copy the vector to the other points on the manifold by *pushing* the vector with \\(dL_g\\) to each \\(g\\) on the manifold.
If we flow all the points on the manifold along these vectors we’ll notice that all the points change in a consistent way! In the case for \\(\mathcal{S}^1\\) they are all rotating around the circle.
Here, we’ve found another invariant flow field. Let’s determine if the vector field is *unchanged* under the combined transformation
$$
(h, v) \mapsto (L_g(h), dL_g(v))
$$
Just like the case for \\(\mathbb{R}^n\\), the points and vector field remain *unchanged*. Furthermore, like \\(\mathbb{R}^n\\) the transformation does not have to be *in the same direction* as the vector field.
Since these vectors don’t all point in the same direction (at least from an extrinsic point of view), we cannot call this a *constant* vector field. However, the vector field is invariant to group transformations, so we will call it an *invariant* vector field.
With these observations, we can state that all Lie Groups have a *continuously symmetric* Tangent Bundle*.* The difference from the euclidean case is that points and (certain) vector fields are invariant under group *transformations* instead of *translations*.
> 💡Although this difference may seem significant at first, it turns that \\(\mathbb{R}^n\\) is actually Lie Group with translation as the group operator! Would you look at that.
As an added bonus, for these *invariant* vector fields, the Euler integration using the exponential map is **exact.** Specifically, for an *invariant* vector field the following closed-form integration holds:
$$
\varphi_X(t) = \text{Exp}_{p}(X(p)t)
$$
> ⚠️ Here in this section, we’ve implied a parallel between *geodesics* on manifolds with a Riemannian Metric and the exponential map on Lie Groups. Technically, we have not defined a notion of a Riemannian Metric for Lie Groups. In this manner, it is possible to define a Riemannian Metric on Lie Groups such that the *geodesic exponential* and the *group exponential* are distinct. Regardless, broadly speaking, in both cases the exponential map helps us move along the manifold in a coherent manner.
As with Euclidean space, we can “recenter” the manifold by using the group operator to move \\(g\\) to the identity \\(e\\) while maintaining the distance to all other points. To do this, we simply apply the operator \\(L_{g^{-1}}\\) to all points on the manifold.
Likewise, we can “subtract” any two points \\(h\\) and \\(g\\) on the manifold by shifting the point we are subtracting to the origin and then using our aforementioned logarithm \\(\text{Log}_e(g^{-1} \circ h)\\).
Leveraging this *continuous symmetry* of Lie Groups, our optimization steps become
– Compute the quantity to minimize *as if* our parameters represent the origin i.e. using \\(\text{Log}_e(g^{-1} \circ h)\\)
– Compute a direction along which the quantity is locally reduced
– Add the minimizing direction to our parameters *as if* our parameters represent the origin i.e. using \\(g \circ \text{Exp}_e(v)\\)
– Repeat until the problem converges
Which makes for a pretty simple algorithm! We really only have to worry about two extra operators \\(\text{Log}_e\\) and \\(\text{Exp}_e\\). Maybe optimizing “on the manifold” isn’t so difficult after all? Let’s apply this *continuous symmetry* concept to the unit sphere to finally cure our Pinhole Obsession.
## Symmetry of the Sphere
Back to our unit sphere! The whole reason we did this in the first place.
Ideally, we’d want the unit sphere to exhibit *continuous symmetry* of the Tangent Bundle so we can take advantage of its benefits:
– Local flow along *invariant* vector fields is the same as a global transformation
– Some arbitrary concept of “origin” or “identity”
– Invariance of points and certain vector fields under global transformations
At first glance, the sphere *looks* fairly symmetric, so constructing an *invariant* vector field should be straightforward. Let’s try to find such a vector field. To start, let’s choose a vector field where all the vectors point at the north pole.
Here we notice that the points on the manifold are generally not all moving in the “same direction.” The points close to the north pole are converging and the points close to the south pole are diverging. This is not an invariant flow field.
Let’s again try to find an invariant flow field but this time choose the vector field where all the vectors are pointing east.
Following the flow, the total set of points remains unchanged*.* This flow field yields a rotation of the sphere. So, the manifold itself exhibits some *continuous symmetry* because rotation leaves the set of points on the manifold unchanged.
> ⭐ If you are wondering why these points flowing east are not moving along great circles, then you are a very astute reader! Remember, that in general using the exponential map \\(\text{Exp}_p(v)\\) to solve the flow \\(\varphi_X(t)\\) of a vector field \\(X\\) is an *approximation.* The true definition is that derivative of the flow \\(\varphi_X'(t)\\) must match the vector field \\(X\\) at every point along the curve.
Does this symmetry extend to the tangent bundle \\(T\mathcal{S}^2\\)? Well, if we swap the north pole and south pole, the vector field is now pointing west! So, the vector field that produces rotations is *not* *invariant* under rotations.
These visualizations, and the aircraft example from beginning of this post point to \\(\mathcal{S}^2\\) not having *continuous symmetry* of its Tangent Bundle. This lack of Tangent Bundle symmetry can be proven rigorously by using the [Hairy Ball theorem](https://en.wikipedia.org/wiki/Hairy_ball_theorem). Unfortunately, this means that we cannot take advantage of **all** the benefits of symmetry when optimizing over \\(\mathcal{S}^2\\). Specifically:
– There is no invariant vector field under a set of global transformations
– We can’t *recenter* a point of interest to do tangent-space computations in a more convenient location
– Each tangent space must be regarded as distinct and not simply *shifted copies* of an origin tangent space
Ultimately, optimizing over a generic asymmetric manifold is a large increase in complexity as opposed optimizing over Euclidean Space or Lie Groups. For each computation, we must perform careful book-keeping to ensure the coherence between:
– Points on the manifold: \\(p \in \mathcal{S}^2\\)
– Vectors in the tangent spaces at each point: \\(v \in T\mathcal{S}^2\\)
– Exponential maps to “move along the manifold”: \\(\text{Exp}_p(v)\\)
– Logarithmic maps to compute the difference between points: \\(\text{Log}_p(q)\\)
If this coherence is not maintained and properly modeled, the optimization is likely to fail. After really digging into the full complexity of optimization over a generic asymmetric manifold, Lie Groups and Euclidean Space seem even more pleasant to work with.
## “Grouping” it All Up
As we can see, optimization over Lie Groups (including Euclidean space) is actually a special case of optimization over a manifold. With *continuous symmetry,* we can actually ignore the effects of the starting point on the exponential operator*. Continuous symmetry* allows us to recenter the manifold on our starting point \\(g\\) (the Lie algebra) and *pretend* that we started at the origin. This is *incredibly handy* and in robotics we use this property a lot!
You’ll notice that in the optimization steps For Lie Groups, we only used the exponential and logarithmic maps at one point: the identity \\(e\\). From a mathematical perspective, this is **the** defining characteristic of Lie Groups. This defining characteristic can be described as an isomorphism between
– The group itself \\(\mathcal{G}\\)
– The Lie Algebra \\(\mathfrak{g} = T_e\mathcal{G}\\)
– The invariant vector fields on \\(\mathcal{G}\\)
There is a number of deep mathematical connections that can be made here, and we encourage the interested reader to learn more. However, for our use-case, it means we can rewrite our exponential map as
$$
\text{Exp}_g(v) = g \circ \text{Exp}_e(v)
$$
If you’ve read the previously mentioned “Micro Lie Theory” paper, you’ll recognize this as the “circle plus” operator i.e. \\(g \oplus v\\). With Lie Groups, there **really** is only one exponential map of concern — the one defined at the identity. This does not hold true for general manifolds. This is why when talking about Lie Groups **the** exponential \\(\text{Exp}\\) map will be described instead of mentioning exponential maps at each point.
So, when using Lie Groups for optimization, we can ignore the specifics about “which tangent space” we’re in. We operate either on the group \\(\mathcal{G}\\), or in the [Lie Algebra](https://en.wikipedia.org/wiki/Lie_algebra) \\(\mathfrak{g}\\). To recall our tools analogy, In the land of Lie Groups, we have two tools to master: a hammer \\(\mathcal{G}\\) and… screwdriver \\(\mathfrak{g}\\).
—
Did you have fun? We sure did. Thanks for going on this deep dive into Differential Geometry and its implications for optimization problems in robotics. Everyone loves Lie groups, no doubt about it.
Of course, if you’re experiencing these concerns in your day-to-day development, it’s probably time you considered working with the Tangram team. We’ve solved these problems so many different ways, on twice as many platforms. It’s our specialty! All this cool math in an easy-to-use package that can shorten your time to market; what’s not to love?


