“The What and Why of Adapter based Parameter Efficient Fine Tuning: Understanding Its Purpose and Significance”
Table of Contents
What is the necessity of fine tuning?
Pre-trained large language models undergo extensive training on vast data from the internet, resulting in exceptional performance across a broad spectrum of tasks. Nonetheless, in most real-world scenarios, there arises a necessity for the model to possess expertise in a particular, specialized domain. Numerous applications in the fields of natural language processing and computer vision rely on the adaptation of a single large-scale, pre-trained language model for multiple downstream applications. This adaptation process is typically achieved through a technique called fine-tuning, which involves customizing the model to a specific domain and task. Consequently, fine-tuning the model becomes vital to achieve highest levels of performance and efficiency on downstream tasks. The pre-trained models serve as a robust foundation for the fine-tuning process which is specifically tailored to address targeted tasks.
What is the conventional way of fine-tuning?
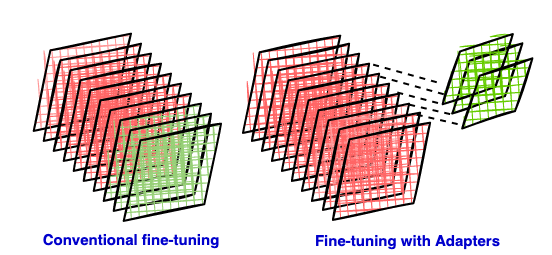
During the conventional fine-tuning of deep neural networks, modifications are applied to the top layers of the network, while the lower layers remain fixed or “frozen”. This is necessary because the label spaces and loss functions for downstream tasks often differ from those of the original pre-trained model. However, a notable drawback of this approach is that the resulting new model retains the same number of parameters as the original model, which can be quite substantial. Nonetheless, creating a separate full model for each downstream task may not be efficient when working with contemporary large language models (LLMs).
In many cases, both the top layers and the original weights undergo co-training. Large language models (LLMs) have reached such immense sizes that fine-tuning even a single layer, let alone the entire model, requires substantial computational resources and can be prohibitively expensive. Take Llama 3.1–8B, for example: it contains 32 layers, excluding embedding and normalization layers, and each layer has about 218 million parameters (combining all projection/attention and MLP layers). Traditional fine-tuning, even if limited to the final layer, thus becomes a costly endeavor. At the end of this blog, we’ll see how this situation can be improved.
How can fine-tuning be made efficient?
Many sought to mitigate this by learning a set of few extra parameters for each new task. This way, we only need to store and load a small number of task-specific parameters in addition to the pre-trained model for each task, greatly boosting the operational efficiency when deployed. This is one of the Parameter-Efficient Fine-Tuning (PEFT) methods and it focuses on fine-tuning only the external modules called Adapters. This approach significantly reduces computational and storage costs.
The advantages of employing parameter-efficient methods for fine-tuning can be articulated in two aspects:
- Regarding disk storage: Fine-tuning solely an adapter module with a limited number of additional parameters necessitates storing only the adapter for each downstream task. This significantly reduces the required storage space for models. It prompts the question of whether maintaining an entire additional copy of LLaMA for each distinct sub-task is truly necessary.
- Concerning RAM: While the exact measurement of the memory footprint considers factors like batch size and various buffers needed during training, the general memory requirement is roughly four times the size of the model. This accounts for gradients, activations, and other elements for each parameter. Fine-tuning a smaller set of parameters alleviates the need to maintain optimizer states for the majority of parameters. During the forward pass, frozen layer weights are used to compute the loss without storing local gradients, saving memory by eliminating the need to save gradients for these layers. During the backward pass, the weights of the frozen layers remain unchanged, which also saves computational resources and RAM, as no calculations are needed for updating these weights.
How does fine-tuning with fewer parameters work?
Li et al.² and Aghajanyan et al.³ showed that the learned over-parametrized models in fact reside on a low intrinsic dimension⁸. This line raises several intriguing questions: What is the intrinsic dimension (ID) of a model? What are over parameterized models? What is the dimension of a model? What is the dimension of an objective function? If ID was so low why do we have such large networks in the first place? How is ID related to fine-tuning, and how to find the ID of a model? These questions will be explored in detail this and the accompanying article.
To pave the way for our discussion on LoRA, here is a quick summary —
- While deep networks may have a large number of parameters, say ’n’, only a small subset of these, say ‘d’ where
d<, truly influences the learning process². The remaining parameters introduce additional dimensions to the solution space, simplifying the training process. The abundant solution space facilitates smoother convergence. 'd' represents what they call the model's ID for that particular task. - Larger models are easier to fine-tune, as they can learn better representations of the training data³ and tend to have a smaller intrinsic dimension (ID).
- Models that are pre-trained for longer periods are easier to fine-tune. Extended pre-training effectively compresses knowledge, reducing the intrinsic dimension (ID)³.
What are adapters and how are they used for fine-tuning?
Adapter modules, as detailed in the paper by Houlsby et al.¹, involves making minor architectural adjustments to repurpose a pre-trained network for a downstream task. Adapter modules are dense layers (full size matrix) introduced between the existing layers of the pre-trained base model which we’ll refer to as ‘adoptee layers’ in this article⁴. In the fine-tuning process, the original network’s weights are kept frozen, allowing only the new adapter layers to be trained, enabling the unchanged network parameters of original network to be shared across multiple tasks. In Part-2, we will explore how adapters integrate into the overall architecture that includes the base model.
Adapter modules possess two key characteristics:
- Compact Size: Adapter modules are relatively smaller than the layers of the original network. This is crucial because the primary purpose of adapters is to save space by storing fewer parameters for each downstream task, rather than replicating the entire base model.
- Minimal Disruption: The initialization of adapter modules should be designed to minimize disruption to training performance in the early stages. This allows the training behavior to closely resemble that of the original model while gradually adapting to the downstream task.
What is LoRA?
LoRA (Low-Rank Adaptation) is a type of adapter technique that involves inserting low-rank matrices as adapters. The authors of LoRA⁶ hypothesized that the adapter modules (the new weight matrices for the adapted task) can be decomposed into low-rank matrices with a very low “intrinsic rank.” They proposed that pre-trained large language models have a low “intrinsic dimension” when adapted to a new task.
The Idea Behind Low-Rank Adaptation
Consider a matrix, denoted as A, with dimensions p x q, which holds certain information. The rank of a matrix is defined as the highest number of linearly independent rows or columns it contains. A concept often introduced in school is that the rank can be easily determined from the matrix’s echelon form. When the rank of matrix A, denoted as r, is less than both p and q, such matrices are termed “rank deficient.” This implies that a full-sized matrix (p x q) isn’t necessary to convey all the information, as it includes a significant amount of redundancy. Consequently, the same information could be conveyed using fewer parameters. In the field of machine learning, its common to work with matrices that are approximated with lower ranks, carrying information in a more condensed form.
Methods for low-rank approximation aim to approximate a matrix A with a another matrix of lower rank. The objective is to identify matrices B and C, where the product of B and C approximates to A (A_pxq ≈ B_pxr × C_rxq), and both B and C have ranks lower than A. We can even pre-define a rank r and accordingly determine B and C. Typically p x r + r x q << p x q , indicating that significantly less space is needed to store the same information. This principle is widely utilized in data compression applications. It’s possible to choose an r that is smaller than the actual rank of A, yet construct B and C in a way that their product approximately resembles A, effectively capturing the essential information. This approach represents a balance between retaining important information and managing spatial constraints in data representation. The reduced number of rows and columns that encapsulate the essential information in a dataset are often referred to as the key features of the data. Singular Value Decomposition (SVD) is the technique employed to identify such matrices B and C for a given matrix A.
The authors of LoRA hypothesize that adapters (weight update matrices) have a low intrinsic rank which refers to the idea that the information contained within the matrix can be represented using fewer dimensions than the the adaptee matrix/layer of the base model might suggest.
Rather than decomposing the selected adaptee matrices through SVD, LoRA focuses on learning the low-rank adapter matrices B and C, for a given specific downstream task.
In our case A_pxq = W_2000x200, B = lora_A and C = lora_B. We approximate a high-dimensional matrix using a lower-dimensional representation. In other words, we try to find a (linear) combination of a small number of dimensions in the original feature space (or matrix) that can capture most of the information in the original matrix. Opting for a smaller r leads to more compact low rank matrices (Adapters), which in turn requires less storage space and involves fewer computations, thereby accelerating the fine-tuning process. However, the capacity for adaptation to new tasks might be compromised. Thus, there’s a trade-off between reducing space-time complexity and maintaining the ability to adapt effectively to subsequent tasks.
Conclusion
Referring back to the example at the beginning of this blog, fine-tuning Llama 3.1–8B with LoRA at a rank of r = 2 reduces the number of trainable parameters to just 5 million — a substantial savings in storage and computational requirements compared to traditional fine-tuning.